*일부 부정확한 내용 있을 수 있다.
채권 가격은 금리 변화=금리 위험(interest rate risk)에 노출되어 있음
금리 변화에 따른 채권가격의 민감도는 채권 수익과 금리 리스크를 계산하는데 매우 중요하며,
이를 측정하기 위해 고안된 것이 듀레이션
이를 측정하기 위해 고안된 것이 듀레이션
•금리 위험의 크기에 영향을 미치는 만기, 액면이자율, 만기 수익률을 하나의 숫자로 종합한 것
•맥컬레이가 처음으로 고안하였으며, 일반적으로 칭하는 듀레이션은 맥컬레이 듀레이션
•실무에서는 이자율탄력성인 수정 듀레이션을 보편적으로 사용
듀레이션의 정의
•1)채권 현금흐름의 가중평균만기
•2)채권 가격의 이자율 탄력성 (수정 듀레이션)
1)채권 현금흐름의 가중평균만기 = 맥컬리 듀레이션

각 기간에 대해 현금흐름의 현재가치란 가중치를 부여해 평균을 구함
•D: 듀레이션 값
•가중치: t시기 현금흐름의 현재가치 PV
•평균을 내는 대상: t
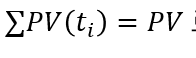
• -> 가중치의 총합이 1임을 알 수 있음
•이를 통해 이해한 듀레이션은 시간 개념으로, 채권 투자자가 초기에 투자한 비용을 회수하는데 걸리는 시간으로 이해 가능

2)채권 가격의 이자율 탄력성 =수정 듀레이션

‐D는 맥컬레이 듀레이션, y는 기간별 수익률
수정 듀레이션을 활용하여 수익률 변화에 따른 채권 가격 변화를 간편하게 추정할 수 있음
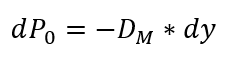
•ex) 표면금리 4%, 액면가 10,000원 채권, 잔존 수정듀레이션 2.7년, 만기수익률 3%, 이자지급 연 1회인 경우
‐ dP_0=-2.7*(-0.01)=0.027
‐P=10,000+0.027*10,000=10,270
듀레이션 및 수정듀레이션은 다음 가정에 기초하여 도출
1.수익률 곡선의 수평
2.수익률 곡선은 항상 평행이동
3.수익률 변화는 크지 않음
위 3가지 가정은 현실적으로 완전히 충족되기 어려우며, 가정과 현실 사이의 괴리가 커질수록 수정듀레이션을 통한 추정치와 실제 가격변화값 사이의 차이도 커짐
이를 보완하기 위해 채권의 convexity(볼록성)을 함께 고려

채권 가격의 이자율 탄력성 = 가격-수익률 곡선의 접선

YTM(매매금리) 와 가격을 상호변환 시켜주는 것이 바로 듀레이션
Duration의 선형성
듀레이션은 선형적
•다양한 듀레이션을 가진 채권들을 포트폴리오로 구성함으로써 원하는 듀레이션을 만들 수 있음
•듀레이션의 선형성은 면역 전략에서 중요하게 사용됨
‐목표 듀레이션에 맞게끔 듀레이션이 다른 각 채권의 가중치를 조정하면 됨

Duration에 영향을 주는 요소들
만기, 액면금리, 수익률, 이자율 기간구조 등이 영향을 줌
•만기가 길어질수록 듀레이션은 커짐
‐일반적으로 만기가 1 unit 올라가면 듀레이션은 1 unit 보다 덜 오름(현금 지급 기간이 분산)
‐무이표채의 경우 만기가 1 unit 올라가면 듀레이션도 1 unit 올라감
•액면금리가 작아지면 듀레이션은 커짐
‐액면금리가 작아지는 것을 먼 기간의 CF의 비중이 커진다고 이해할 수 있음
‐무이표채의 경우 듀레이션은 만기와 같음
•YTM이 작아지면 듀레이션은 커짐
‐먼 기간의 CF가 덜 할인되기 때문에 가중평균 만기가 길어진다고 이해할 수 있음
•Yield curve의 기울기가 낮아질수록 듀레이션은 커짐
*금리가 상승하면 듀레이션은 낮아짐: 이자율 변화에 따른 가격 변화폭이 둔화되므로
채권의 볼록성(Convexity)
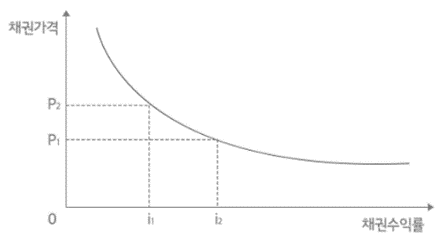
가격과 수익률 간의 관계를 나타내는 함수는 원점에 대해 볼록한 곡선
•듀레이션은 1계미분(선형근사)이지만, 금리와 채권가격 사이의 관계는 볼록한 곡선으로 나타나므로 듀레이션만으로는 오차가 발생
•듀레이션을 통한 선형 근사식의 한계를 보완하기 위해 2계미분을 도입
•이자율 변화가 클 경우, 듀레이션과 convexity(볼록성)을 고려하여 금리 변화에 따른 채권 가격의 변동폭 계산 필요
•같은 조건이면 convexity가 큰 채권이 좋음
‐금리 하락에는 가격이 크게 상승하고, 금리 상승에는 가격이 적게 하락

컨벡시티 정의와 2차 테일러 근사

말킬의 채권 가격 정리
1.채권가격과 수익률(YTM)은 역의 관계(P↑, y↓)
2.만기가 긴 채권이 만기가 짧은 채권보다 수익률 변동에 따른 가격 변동성이 더 큼
3.수익률 변동에 따른 가격 변동성은 만기가 길수록 체감하면서 증가
4.만기가 일정할 때 수익률 하락으로 인한 가격 상승폭이 같은 폭의 수익률 상승으로 인한 하락폭보다 더 큼
5.표면이자율이 낮은 채권일수록 일정한 수익률 변동에 따른 가격 변동폭이 더 큼
●2,3,5는 듀레이션에 관련된 설명 ,4는 컨벡시티에 관련된 설명으로 이해해볼 수 있다.
'매크로 노트 & 투자 아이디어 > 채권 & FICC' 카테고리의 다른 글
| QE를 하는데 상업은행이 채권을 사는 이유 (0) | 2022.08.15 |
|---|---|
| 간단한 채권 가이드 - 채권 금리는 인플레이션과 성장률의 함수 (0) | 2022.08.06 |
| 인플레이션 피크아웃? 그 다음은 어디일까 (0) | 2022.08.02 |
| 아주 단순한 채권 투자 가이드 (0) | 2022.07.31 |
| 폴 크루그먼: 왜 시장은 악재에 의연한가 (07.18) (0) | 2022.07.18 |