*개념이 앞뒤로 왔다갔다해서 좀 헷갈린다. 이해한 만큼 정리해본다.
선도금리(forward rate) 기간구조를 결정하는 3가지 요인
1.시장의 금리 기대
2. 채권 리스크 프리미엄
3.convexity bias
순수기대 가설이 지켜질 때, 모든 국채는 동일한 near-term 기대수익률을 가진다.( 모든 리스크 프리미엄 =0)
단기 기대수익률이 모든 만기간에 같다면, 초기 금리 차이가 시장의 금리 기대로 인한 예상된 자본 손익을 상쇄해야만 한다.
예를 들어, 시장이 금리가 상승할 것을 기대하며 장기채가 자본손실을 볼 것이라 생각한다면, 장기채는 1기간의 채권보다 초기 금리 이점이 있어야만 한다.
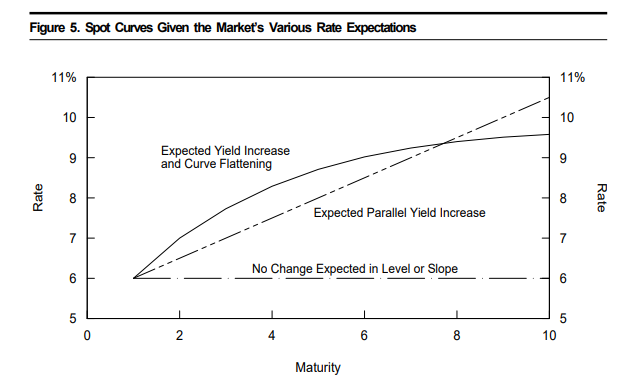
그러므로, 금리 상승 기대는 현재의 일드커브가 우상향하도록 한다.
비슷한 방식으로 미래 커브의 플래트닝/스티프닝 기대는 현재 일드커브의 곡률(curvature)에 영향을 미친다.
이하의 두 서술은 구분되어야 한다. 두 서술은 순수기대 가설이 충족될 때만 동일하다.
1.포워드forward가 상승하는 spot 금리를 암시한다
2.시장이 상승하는 spot 금리를 예상한다
1번 서술은 미래 spot 금리의 break-even level로서의 포워드 금리의 역할을 뜻한다. 방법론적으로, 포워드가 암시하는 다음기까지의 spot 금리 변화는 모든 정부채가 동일한 1기 수익을 얻게한다.
spot 금리 커브가 우상향할 때면 언제나 포워드는 상승하는 금리를 암시한다. 다시말해, 금리 상승이 장기채의 초기 금리 이점을 상쇄하기 위해 필요하다.
그러나 이는 시장이 꼭 금리 상승을 기대한다는 뜻은 아니다. 우상향하는 spot 금리 커브는 양의 채권 리스크 프리미엄을 반영한 결과일 수도 있다.(무위험의 1기간 채권 대비 장기채 보유를 위해 더 많은 near-term 수익률 필요) 포워드 금리가 암시하는 spot금리 변화는 대략적으로 spot 금리 변화와 같은데, 오직 제약적인 순수 기대 가설이 사실일 때만 그렇다.
이 글에는 순수 기대 가설이 여러모로 역사적 경험과 맞지 않는 사례들을 제시할 것이다. 포워드 금리는 미래 spot을 예측하는 나쁜 도구라는 것도 보여줄 것이다. 사실 장기 금리는 포워드 금리에 의해 암시된 방향에 반대되게 움직이는 경향이 있다. 또한 포워드 금리 구조에 암시된 기대와 시장 참가자들 대상으로 한 설문에서의 기대를 대조시킬 것이다. 이 비교는 포워드 금리가 시장의 금리 기대를 상방 편향을 갖고 측정하는 도구임을 보여주는데, 시장은 단기채보다 장기채를 보유하는데 더 많은 수익률을 요구하기 때문이다.
이 섹션에서는 spot, 포워드, 그리고 포워드의 break-even 금리로서의 역할을 다룰 것이다.
포워드 금리의 계산:
spot 금리는 무이표채(zero coupon bond)와 같은 단일 현금흐름의 할인률이다. 이표채는 무이표채의 묶음으로 볼 수 있다.



forward 금리는 오늘 계약한 두 개의 미래 시점 사이의 대출 금리로 볼 수 있다. 이 금리는 거래된 선도 계약에 명시적으로 드러날 수도 있고, 현재의 spot 금리 커브에 의해 암시될 수도 있다.
spot 금리는 1년 forward 금리의 기하 평균이다.
*appendix) f_n,n+1의 1기간 포워드 금리는 s_n, s_n+1의 연속된 스팟 금리의 미분으로 생각해볼 수 있다.
포워드 금리 f_m,n를 러프하게 표현하면
=현 시점에서 m년 뒤의 (현 시점t0 기준의) n년 스팟 금리
= m년 뒤 스팟금리로 사서 n년후 스팟금리로 팔 때 수익
*실제로는 3개월, 1년 단위 컴파운딩이 사용되어 연율화를 위한 표현이 더 들어간다. 글에서는 1년 ,1기간 단위를 혼용하여 적는 점 양해를 구한다.
fig1

fig 2

a : spot
b: 1년 포워드
c: 내재 spot 1년 포워드 (implied spot rate curve 1-year forward), 현 시점에서 1년 이후의 스팟 금리 기대
d = c-a : 내재 spot 변화 (implied change in the spot rate), 항상만기(constant maturity) n년 스팟 금리의 기대되는 변화
b와 c는 둘 다 포워드라는 명칭으로 혼용된다. 아랫첨자로 구분. 블로그에는 아래첨자 넣기 어려워 언더바 이후의 숫자로 표기.
b: f_0,1, f_0,2 ..
c: f_1,2, f_1,3...
d는" 포워드가 상승하는 금리를 암시함"을 보여준다. 이하는 앞선 내용의 반복
이는 시장이 금리가 상승한다는 것을 말하는 것이 아니다. 포워드는 spot 커브가 1년간 얼마나 변해야 모든 채권이 동일한 보유기간 수익을(holding period return) 갖게 되는지를 말해준다.
보유기간 수익 : 채권의 초기 금리 + 금리 변동에 따른 자본 손익
예) 오늘 spot 커브가 우상향하면, 장기채는 1기간의 채권 대비 초기 금리 이점이 있다. 보유기간 수익률이 동일해지기 위해서는 장기채는 그만큼의 자본손실을 봐야 한다. 포워드는 정확히 얼마나 장기금리가 상승해서 그러한 자본손실을 겪게 될지 보여준다.
금리 변화가 아닌 금리 수준(level)관점에서 표현하자면, c =내재 spot 1년 포워드는 모든 정부채가 1년간 동일한 보유기간 수익을 얻게 하는 미래의 스팟 금리다.
더 나아가, 동일한 보유기간수익은 현재의 1년 할인채 수익률과 같아야한다.

수식 4 :
수식 3에 m =1을 삽입
좌변: n년 spot을 현재 매수, 1년 뒤에 f_1,n의 포워드 금리로 매도
우변: 무위험 수익인 현재 1년 할인채 금리
* n년 스팟매수가: 100/(1+s_n)^n
n년 스팟 1년 후 매도가 : 100/(1+f_1,n)^(n-1)
n년 스팟 매수/ 1년 후 매도 손익 = 스팟 1년후 매도가/ 현재 매수가
=1년 할인채 수익률
Fig1 수치 예시)
f_1,2
s_1 = 6%
s_2 = 7%
궁금한 것: s_2의 1년뒤 가격=f_1,2가 얼마가 되어야 보유수익률이 6% =s_1이 될까
-> (1+f_1,2)^(2-1) = (1+s_2)^2/(1+s_1)^1
f_1,2 = (1+7%)^2/(1+6%) -1 = 8.01%
*내재 spot 변화(fig1 d와 관련)의 세밀한 분류
1)개별 채권 금리가 얼마나 변해야(상승해야) 기존의 이자수익 이점을 상쇄할 수 있는지
(yield advantage, break-even yield change needed to offset carry )
f_1,2 - s_1= 2.01%
수식4의 내용의 반복. 다시 부언하자면 순수기대가설을 전제로 한 내용이다.
2)항상만기(constant maturity) 채권 금리가 어떻게 변동해야 만기별 채권 금리의 hpr(보유기간수익)이 동일해지는지.
f_1,2 - s_2 = 1.01%
*fig 1 d는 2)의 항상만기 개념에 해당
1)과 구분하면 스팟 커브 자체의 이동으로 표현
f_1,2 -s_1과 f_1,2-s_2의 차이 = s_2 - s_1 -> 롤링 수익률
*1),2)의 분류를 정확히 구분해야 한다.
fig3
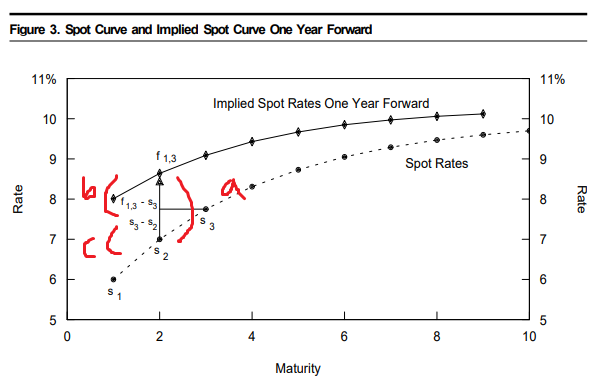
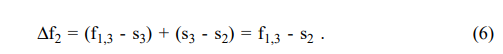
*그래프 예시로 반복 설명
a: f_1,3 -s_2 :
항상만기 2년 스팟 금리 변화 기대치 , break-even yield change ( fig 1의 d, 내재 포워드 변화 )
b: f_1,3 - s_3 :
break-even yield change needed to offset carry, yield advantage
c: s_3 - s_2 :
rolldown yield change
*a= b+c로 분해
항상만기 n년 스팟의 1기간 후 금리 변화 기대치 = 현재 (개별) n년 스팟의 1기간 후 금리 변화 기대치 + 롤링 수익률
수치 예시)
s_1=6%, s_2 = 7%, s_3 = 7.75%, dur_2 = 2로 주어졌다면
->b: yield advantage 성분 : (s_3 -s_1) / dur_2 = (7.75-6.00)/2 % = 0.875% (뒤에 설명)
c: roll down 성분 = s_3 - s_2 = (7.75-7.00) % = 0.75%
a : d_f_2 = f_1,3 - s_2 = b+c = 1.625%
b : yield advantage 성분 :
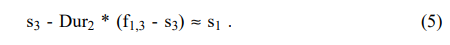
3년 스팟을 사서 1년뒤에 현 시점 기준 포워드 금리로 팔 때 손익
-> 이자수익 s_3 + 자본손익
= 1기간 보유수익률 s_1
수식 5를 재정렬하면 f_1,3 - s_3 = (s_3-s_1)/Dur_2 (정확히는 약등호)
3년 스팟을 사고 1년 스팟을 팔면서 zero cash 포지션을 만드는 것으로 생각해볼 수 있음. (수익률 곡선이 우상향하므로) s_3 - s_1는 막대한 양의 이자수익을 준다.
포지션의 수익은 이자수익(s_3-s_1) + 더 긴 만기 할인채(s_3)의 금리 변동이다.
항상만기의 s_2금리가 f_1,3보다 1년간 더 상승할 때 손실을 본다. (?)
1기간 포워드 & 내재 spot 1기간 포워드(각각 fig 1의 b,c)간의 관계:
1기간 포워드 커브가 스티프닝 되어있을 수록, 내재 스팟 1년 포워드 커브도 스티프닝 되어야만 한다.
1기간 포워드 커브 스티프닝 -> 장기채의 단기채 대비 막대한 롤링 수익률 이점 반영되어 있는 것(도출은 appendix 참조) -> 내재 스팟 1기간 포워드도 롤링수익률 이점만큼 상승해야 함
*커브 플래트닝 포지션에 대한 Break-even 수익률 변화
투자자가 1년 시계의 플래트닝(바벨-불렛) 포지션 형성:
3년 할인채 매도/ 1, 5년 할인채 매수
->이 포지션의 손익은 역캐리, 롤링의 2가지 측면에서 생각해봐야 한다.
1. 역캐리(negative carry)
:해당 포지션이 수익을 거두려면 미래 스팟 커브의 플래트닝이 역캐리를 뛰어넘는 자본 수익을 가져다 주어야 한다.
일드커브가 오목(concave)할 때,
3년 할인채에서 1년 할인채로 가는 것의 수익률 하락분> 3년에서 5년으로 갈 떄의 수익률 상승분
예시) 0.5* (s_1 - s_3 ) + 0.5 * ( s_5 - s_3) =
0.5 * (6.00 - 7.75) + 0.5*( 8.73 - 7.75) = -0.39
내재 1기간 포워드 스팟 커브는 해당 스프레드 포지션의 break-even 수준을 알려준다.
현재 스팟 커브의 곡률이 높을 수록 ( more curvature), 즉 1년이나 5년 스팟이 3년보다 낮을 수록, 플래트닝 포지션의 매력도는 역캐리로 인해 낮아진다. 그리고 포워드 역시 더 많은 플래트닝을 반영한다.
스팟커브가 선형이라면 플래트닝 포지션은 캐리 측면의 예상되는 손실이 없다. 포워드 역시 플래트닝을 전혀 반영하지 않을 것이다.
2.롤링 수익률
-스팟 커브가 오목하면, 롤다운 수익 이점이 불렛의 수익률 이점을 더한다. (3년 할인채 롤다운 수익 > 5년 할인채 롤다운 수익)
그래서 fig4에서 보듯, 롤링 일드 커브 (= 1기간 포워드 커브)는 스팟 커브보다 더욱 오목하다. (이유 잘 모르겠음)
롤링 일드 커브= 1기간 포워드 커브인 이유는 앞에서 서술했듯,
f_n,n+1의 1기간 포워드 금리는 s_n, s_n+1의 연속된 스팟 금리의 미분이기 때문. 기하평균 미분 관련 성질 생각해보면 됨
(역캐리와 롤다운 수익 차이를 상쇄하기 위해 필요한) 내재 플래트닝의 정도는 롤링 수익률 커브의 곡률curvature에 달려있다.
fig4
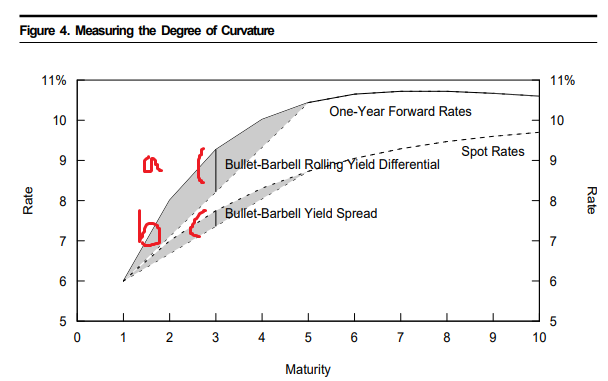
a: 바벨-불릿 간의 롤링 수익률 차이differential
1년 포워드 금리 곡선을 f(x)라고 하면, a= f(3) - (f(1)+f(5))/2
b: 바벨-불릿 수익률 스프레드
b가 클 수록 바벨 포지션의 비용이 "비싸다". 위에서 말한 역캐리에 해당.
더 많은 플래트닝이 나타나야 break-even해지기 때문이다.
= a가 -이면 b만큼 스프레드가 축소(-)되어야 break-even해진다.
예시) fig1의 수치를 사용하면
*1년, 5년을 사고 3년을 매도한 포지션의 초기 롤링 수익률 차이 (fig4 a)
= 0.5*f_0,1 + 0.5*f_4,5 - 1*f_2,3
= -1.05
즉 3년의 롤링 수익률 상대 이점으로 해당 포지션은 초기 롤링수익률 손해를 보게 된다.
* 2년-4년 스프레드가 1년간 52bp (fig4 b) 축소되어 자본수익을 거두어야, 해당 포지션의 초기 롤링수익률 손해를 상쇄할 수 있음
( f_1,5 - s_4) - (f_1,3 - s_2) = 1.12 - 1.64 = -0.52
fig1의 d열( 항상만기(constant maturity) n년 스팟 금리 기대 변화) 참조.
fig5
e7
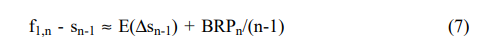
fig6
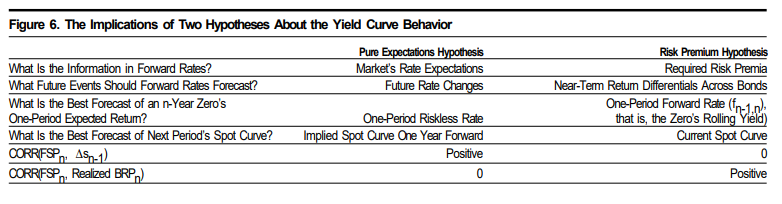
fig7

fig8
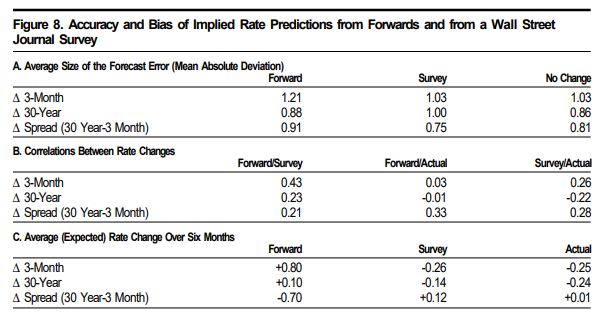
fig9
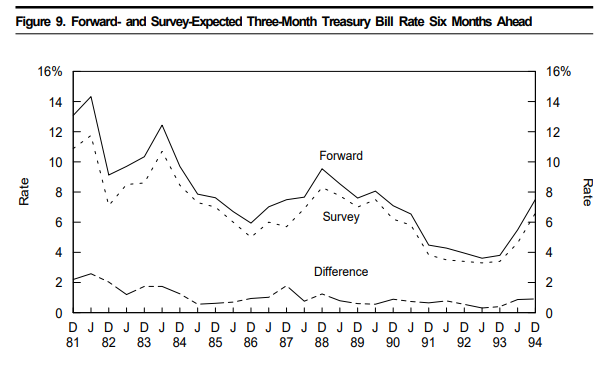
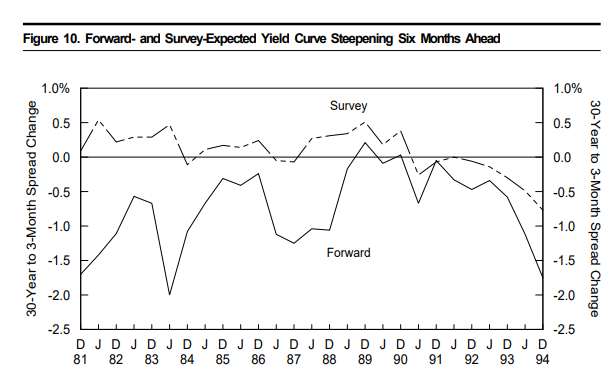
fig10
e8

e9

e10
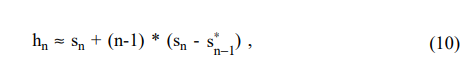
e11
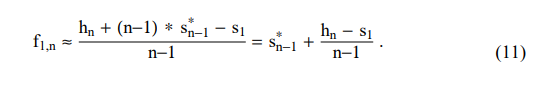
e12
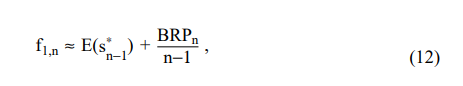
e13
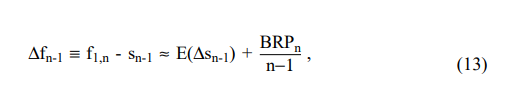
e14
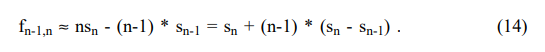
e15
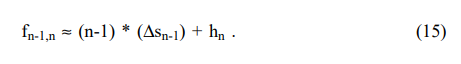
e16
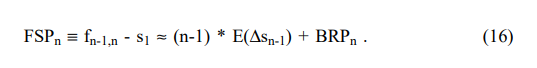
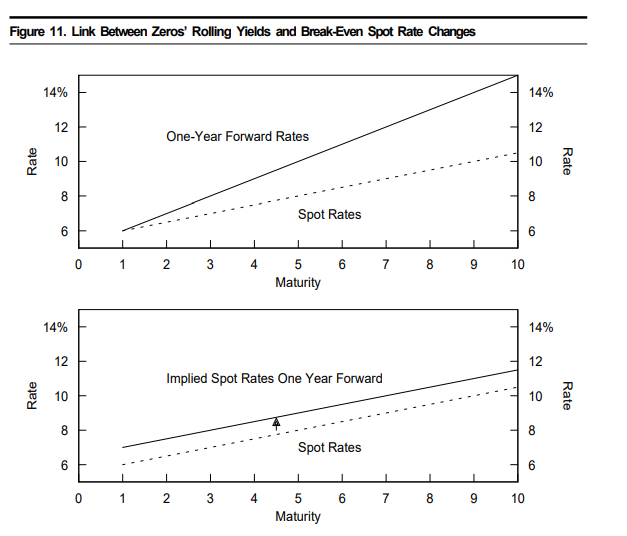
fig11
'매크로 노트 & 투자 아이디어 > 채권 & FICC' 카테고리의 다른 글
| ZQ선물 분산, 집중경향 (0) | 2024.04.09 |
|---|---|
| 효율적인 채권 패시브ETF 운용? (0) | 2024.03.28 |
| 기간 프리미엄 (Term premium) 개요 (0) | 2024.03.08 |
| 채권 가이드 : Drivers of Bond Yields (0) | 2024.03.07 |
| 미국 주거(shelter) 인플레이션 & Lagging 이슈 (0) | 2024.02.27 |